✔ 최소 공통 조상
최소 공통 조상이란?
- 트리 그래프에서 임의의 두 노드를 선택했을 때
두 노드가 각각 자신을 포함해 거슬러 올라가면서 부모 노드를 탐색할 때 처음 공통으로 만나게 되는 부모 노드 - 일반적인 최소 공통 조상 찾기와 최소 공통 조상 빠르게 찾기가 존재
- 트리의 높이가 크지 않을 때는 일반적인 최소 공통 조상 찾기 사용 (1개씩 올라가기)
- 트리의 높이가 커질 경우, 시간 제약 문제가 직면할 수 있으므로 최소 공통 조상 빠르게 찾기 사용 (2^K씩 올라가기)
일반적인 최소 공통 조상 구하기
- 부모 노드와 깊이 저장 배열 만들기
- 루트 노드에서 탐색을 시작해 각 노드의 부모 노드와 깊이를 저장함
- 이때 탐색은 DFS 또는 BFS를 이용
- 선택된 두 노드의 깊이가 다를 경우, 더 깊은 노드의 노드를 부모 노드로 1개씩 올려 주면서 같은 깊이로 맞춤
- 이때 두 노드가 같으면 해당 노드가 최소 공통 조상이므로 탐색을 종료
- 두 노드가 같지 않다면, 깊이가 같은 상태에서 동시에 부모 노드로 올라가면서 두 노드가 같은 노드가 될 때까지 반복


최소 공통 조상 빠르게 구하기
- 부모 노드 저장 배열 만들기
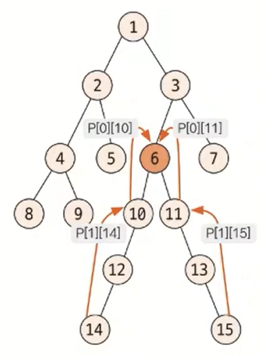
- 기존에 자신의 부모 노드만 저장해 놓던 방식에서 2^K번째 위치의 부모 노드까지 저장하도록 함
- K = 0번째 배열은 DFS 또는 BFS를 이용해 탐색해 초기화한 후,
부모 노드 배열의 점화식을 이용해 K를 1개씩 증가시키면서 나머지 배열을 채움 - P[K][N] = N번째 노드의 2^K번째 부모의 노드 번호일 때, P[K][N] = P[K - 1][P[K - 1][N]]
- 즉, N의 2^K번째 부모 노드는 N의 2^(K-1)번째 부모 노드의 2^(K-1)번째 부모 노드라는 의미
- 배열에서 K의 범위는 트리의 깊이 > 2^K를 만족하는 최댓값
- 예)
P[2][10] = 10번 노드의 2^2번째 부모 노드 = 10번 노드의 4번째 부모 노드
P[1][P[1][10]] = (10번 노드의 2^1번째 부모 노드)의 2^1번째 부모 노드 = 10번 노드의 2번째 부모 노드의 2번째 부모 노드
- 선택된 두 노드의 깊이 맞추기
- 기존에 한 단계씩 맞췄던 깊이를 2^K 단위로 넘어가면서 맞춤
- 예) 두 노드의 깊이 차이가 4일 경우
깊이를 맞추기 위해 4 = 2^2이므로 K = 2이므로 P[2][N]으로 노드를 이동 - 만약 높이 차이가 2048일 경우, 2048 = 2^11이므로 K = 11을 이용해 P[11][N]으로 한 번에 이동하여 깊이 맞추기 가능
- 최소 공통 조상 찾기
- 기존에 한 단계씩 맞췄던 공통 조상을 찾는 작업을 2^K 단위로 점프하면서 맞춤
- K값을 1씩 감소하면서 부모 노드 저장 배열을 이용해 최초로 두 노드의 부모가 달라지는 값을 찾음
- 반복문이 종료된 후 이동한 두 노드가 같은 노드라면 해당 노드가, 다른 노드라면 바로 위의 부모 노드가 최소 공통 조상이 됨





더보기
Do it! 알고리즘 코딩테스트 with JAVA
'Coding Test > Java 알고리즘 개념' 카테고리의 다른 글
| [동적 계획법] 동적 계획법 (0) | 2023.08.12 |
|---|---|
| [조합] 조합 (0) | 2023.08.11 |
| [트리] 세그먼트 트리 (인덱스 트리) (0) | 2023.08.08 |
| [트리] 이진 트리 (0) | 2023.08.06 |
| [트리] 트라이 (0) | 2023.08.06 |
