✔ 트리
트리(Tree)란?
- 노드와 엣지로 연결된 그래프의 특수한 형태
- 비선형 자료구조이며 계층적 관계를 표현
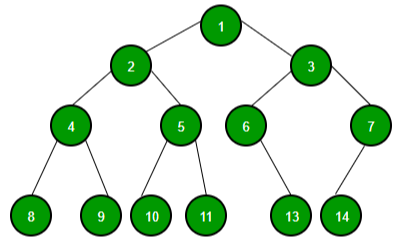
트리의 특징
- 순환 구조(사이클)를 지니고 있지 않고, 1개의 루트 노드가 존재함 (방향성이 있는 비순환 그래프)
- 루트 노드를 제외한 노드는 단 1개의 부모 노드를 가짐
- 노드가 N개인 트리는 항상 N - 1개의 간선을 가짐
- 트리에서 임의의 두 개의 노드를 연결하는 경로는 유일함
- 트리를 순회하는 방식으로는 전위 순회, 중위 순회, 후위 순회, 레벨 순회가 존재
- 트리의 부분 트리 역시 트리의 모든 특징을 따름
트리의 구성 요소
- 노드 : 데이터의 index와 value를 표현하는 요소
- 엣지 (간선) : 노드와 노드의 연결 관계를 나타내는 선
- 루트 노드 : 트리에서 가장 상위에 존재하는 노드
- 부모 노드 : 두 노드 사이의 관계에서 상위 노드에 해당하는 노드
- 자식 노드 : 두 노드 사이의 관계에서 하위 노드에 해당하는 노드
- 리프 노드 (단말 노드) : 트리에서 가장 하위에 존재하는 노드, 자식 노드가 없는 노드 ↔ 내부 노드 (비단말 노드)
- 서브 트리 : 전체 트리에 속한 작은 트리
- 레벨 : 트리의 각 층으로 레벨은 1부터 시작
- 높이 : 트리의 최고 레벨
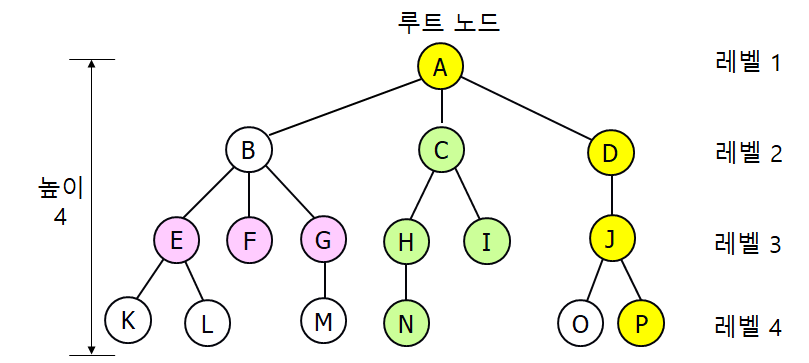
이진 트리(Binary Tree)란?
- 각 노드의 자식 노드의 개수가 2 이하로 구성되어 있는 트리
- 루트 노드를 중심으로 두 개의 서브 트리로 나뉘어지며 나뉘어진 두 서브 트리도 모두 이진 트리이어야 함
- 이진 트리의 종류로는 편향 이진 트리, 포화 이진 트리, 완전 이진 트리가 존재

이진 탐색 트리(Binary Search Tree)란?
- 효율적인 탐색을 위한 저장 방법으로 이진 트리에 데이터를 저장
- 이진 탐색과 연결 리스트를 합하여 장점을 모두 얻기 위해 고안된 것
- 이진 탐색 트리의 노드에 저장된 키는 유일하며
부모의 키는 왼쪽 자식 노드의 키보다 크고, 오른쪽 자식 노드의 키보다 작아야 한다는 규칙을 가지고 데이터가 저장됨 - 평균적으로 시간 복잡도는 O(logN)을 가지지만, 편향 이진 트리일 경우 한 쪽으로만 노드가 추가되어 시간 복잡도 O(N)을 가짐
- 중위 순회로 순회하며 정렬된 순서를 읽게 됨
- 균형 잡힌 트리로 재조정하기 위한 Rebalancing 기법이 존재

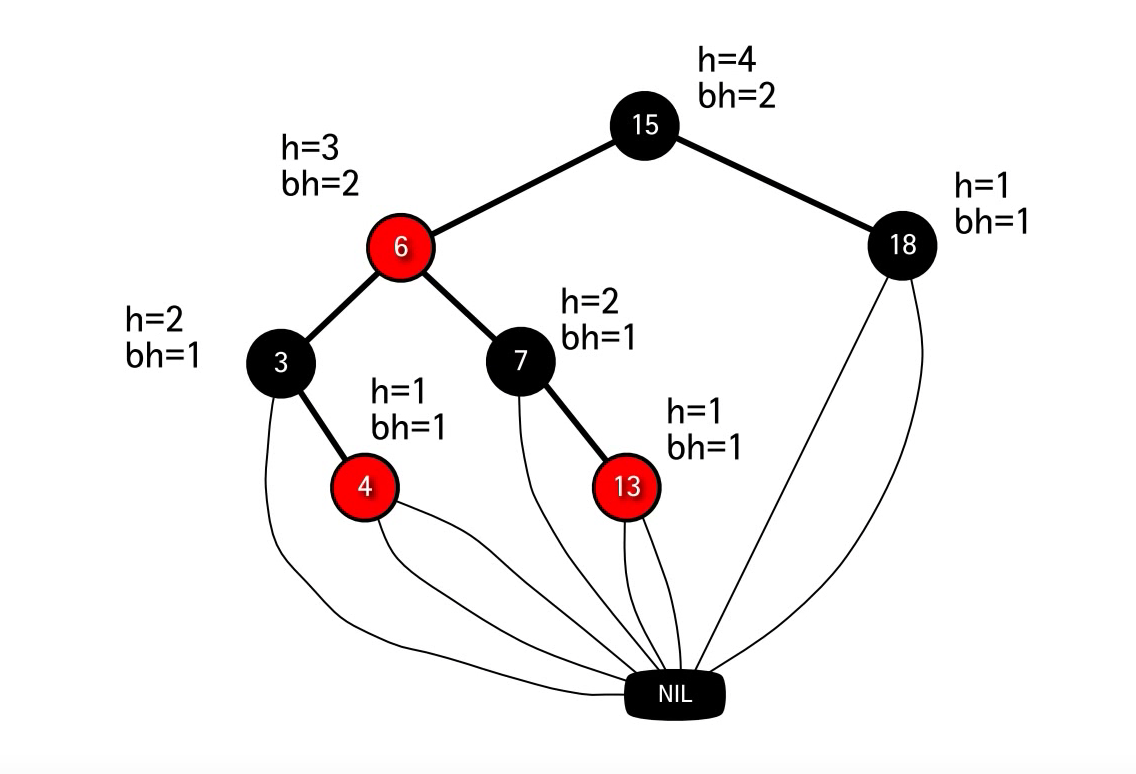
레드 블랙 트리(Red-Black Tree)란?
- 이진 검색 트리를 기반으로하는 트리 형식의 자료구조
- 각 노드는 레드 또는 블랙 색깔을 가지며, 루트 노드와 리프 노드는 블랙을 가지게 됨
- 각 노드에 대하여 노드로부터 리프 노드까지의 단순 경로는 모두 같은 수의 블랙 노드를 포함하게 됨
- 이진 검색 트리의 삽입, 삭제 연산 과정에서 발생할 수 있는 문제점을 해결하기 위해
루트 노드부터 리프 노드까지 모든 경로 중 최소 경로와 최대 경로의 크기 비율을 2보다 크지 않도록 하여 balanced 상태로 만듦 - 균형 잡힌 트리 상태이므로 O(logN)의 시간 복잡도를 가짐 (h가 트리의 높이일 때, O(h))
B-트리란?
- 데이터베이스, 파일 시스템에서 널리 사용되는 트리 자료구조
- 이진 트리를 확장해서, 더 많은 수의 자식을 가질 수 있도록 함
- 자식 수에 대한 일반화를 진행하면서, 하나의 레벨에 더 저장되는 것 뿐만 아니라
트리의 균형을 자동으로 맞춰주는 로직까지 가지므로 단순하고 효율적이며, 완전히 균형을 맞춘 트리 - 각 노드에는 key와 data가 모두 들어가 저장되게 됨
- 루트 노드는 적어도 2개 이상의 자식을 가져야 하며, 노드의 자료수가 N이면, 자식 수는 N + 1이어야 함
또한 입력 자료는 중복될 수 없음
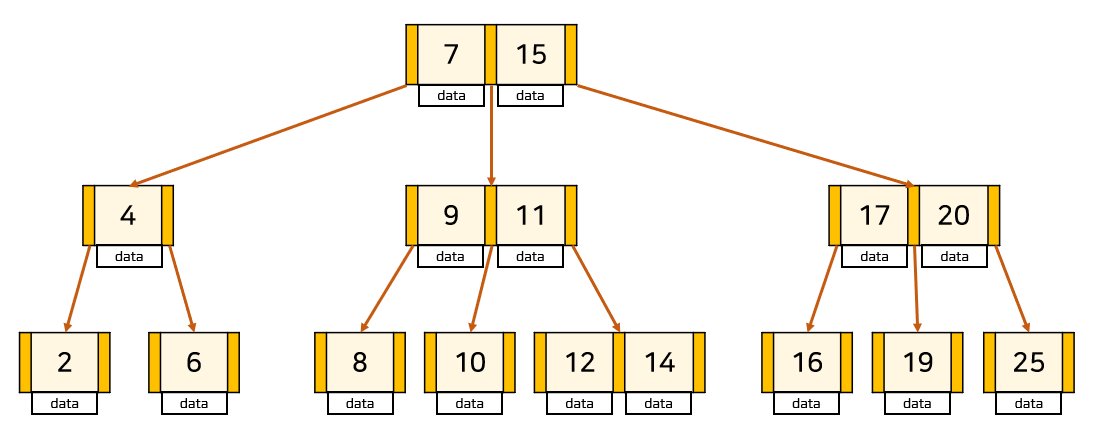
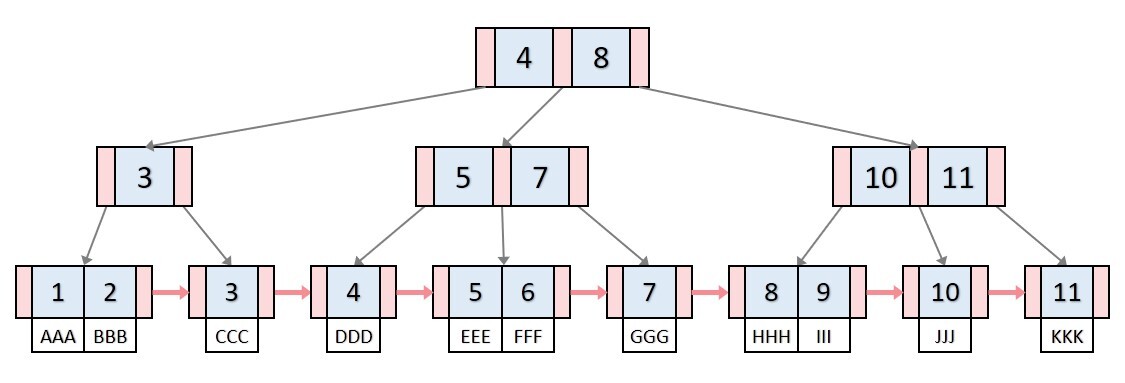
B+트리란?
- B-트리에서 데이터의 빠른 접근을 위한 인덱스 역할을 하는 비단말 노드가 추가된 트리 자료구조
- 각 노드에는 key만 들어가고, data는 리프 노드에만 존재하게 됨
- 기존의 B-트리(index 부분)와 데이터의 연결리스트(순차 데이터 부분)로 구현된 색인구조로
인덱스 부분의 key 값은 리프 노드에 있는 key 값을 직접 찾아가는데 사용하게 됨
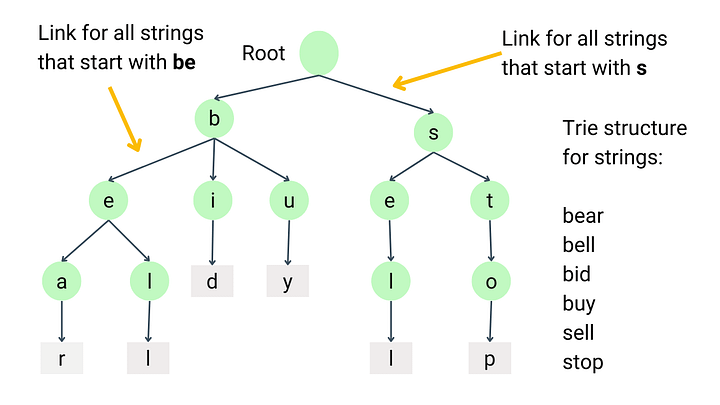
트라이(Trie)란?
- 문자열 검색을 빠르게 실행할 수 있도록 설계한 트리 형태의 자료구조
- Digital Tree, Radix Tree, Prefix Tree라고도 불림
- 단어들을 사전의 형태로 생성한 후 트리의 부모 자식 노드 관계를 이용해 검색을 수행
- 각 노드는 하나의 알파벳인 key와 그 key에 해당하는 자식 노드인 value 값을 가지게 됨
- 문자 종류의 개수인 N에 따라 N진 트리가 결정됨
- 루트 노드는 항상 빈 문자열을 뜻하는 공백 상태를 유지
- 루트 노드를 제외한 노드의 자손들은 해당 노드와 공통 접두어를 가지게 됨
'Tech Interview > Data Structure' 카테고리의 다른 글
| [Data Structure] 그래프 (Graph) (0) | 2023.11.30 |
|---|---|
| [Data Structure] 해시 (Hash) (0) | 2023.11.28 |
| [Data Structure] 힙 (Heap) (0) | 2023.11.25 |
| [Data Structure] 큐 (Queue) (0) | 2023.11.24 |
| [Data Structure] 스택 (Stack) (0) | 2023.11.22 |
✔ 트리
트리(Tree)란?
- 노드와 엣지로 연결된 그래프의 특수한 형태
- 비선형 자료구조이며 계층적 관계를 표현

트리의 특징
- 순환 구조(사이클)를 지니고 있지 않고, 1개의 루트 노드가 존재함 (방향성이 있는 비순환 그래프)
- 루트 노드를 제외한 노드는 단 1개의 부모 노드를 가짐
- 노드가 N개인 트리는 항상 N - 1개의 간선을 가짐
- 트리에서 임의의 두 개의 노드를 연결하는 경로는 유일함
- 트리를 순회하는 방식으로는 전위 순회, 중위 순회, 후위 순회, 레벨 순회가 존재
- 트리의 부분 트리 역시 트리의 모든 특징을 따름
트리의 구성 요소
- 노드 : 데이터의 index와 value를 표현하는 요소
- 엣지 (간선) : 노드와 노드의 연결 관계를 나타내는 선
- 루트 노드 : 트리에서 가장 상위에 존재하는 노드
- 부모 노드 : 두 노드 사이의 관계에서 상위 노드에 해당하는 노드
- 자식 노드 : 두 노드 사이의 관계에서 하위 노드에 해당하는 노드
- 리프 노드 (단말 노드) : 트리에서 가장 하위에 존재하는 노드, 자식 노드가 없는 노드 ↔ 내부 노드 (비단말 노드)
- 서브 트리 : 전체 트리에 속한 작은 트리
- 레벨 : 트리의 각 층으로 레벨은 1부터 시작
- 높이 : 트리의 최고 레벨

이진 트리(Binary Tree)란?
- 각 노드의 자식 노드의 개수가 2 이하로 구성되어 있는 트리
- 루트 노드를 중심으로 두 개의 서브 트리로 나뉘어지며 나뉘어진 두 서브 트리도 모두 이진 트리이어야 함
- 이진 트리의 종류로는 편향 이진 트리, 포화 이진 트리, 완전 이진 트리가 존재

이진 탐색 트리(Binary Search Tree)란?
- 효율적인 탐색을 위한 저장 방법으로 이진 트리에 데이터를 저장
- 이진 탐색과 연결 리스트를 합하여 장점을 모두 얻기 위해 고안된 것
- 이진 탐색 트리의 노드에 저장된 키는 유일하며
부모의 키는 왼쪽 자식 노드의 키보다 크고, 오른쪽 자식 노드의 키보다 작아야 한다는 규칙을 가지고 데이터가 저장됨 - 평균적으로 시간 복잡도는 O(logN)을 가지지만, 편향 이진 트리일 경우 한 쪽으로만 노드가 추가되어 시간 복잡도 O(N)을 가짐
- 중위 순회로 순회하며 정렬된 순서를 읽게 됨
- 균형 잡힌 트리로 재조정하기 위한 Rebalancing 기법이 존재

레드 블랙 트리(Red-Black Tree)란?
- 이진 검색 트리를 기반으로하는 트리 형식의 자료구조
- 각 노드는 레드 또는 블랙 색깔을 가지며, 루트 노드와 리프 노드는 블랙을 가지게 됨
- 각 노드에 대하여 노드로부터 리프 노드까지의 단순 경로는 모두 같은 수의 블랙 노드를 포함하게 됨
- 이진 검색 트리의 삽입, 삭제 연산 과정에서 발생할 수 있는 문제점을 해결하기 위해
루트 노드부터 리프 노드까지 모든 경로 중 최소 경로와 최대 경로의 크기 비율을 2보다 크지 않도록 하여 balanced 상태로 만듦 - 균형 잡힌 트리 상태이므로 O(logN)의 시간 복잡도를 가짐 (h가 트리의 높이일 때, O(h))

B-트리란?
- 데이터베이스, 파일 시스템에서 널리 사용되는 트리 자료구조
- 이진 트리를 확장해서, 더 많은 수의 자식을 가질 수 있도록 함
- 자식 수에 대한 일반화를 진행하면서, 하나의 레벨에 더 저장되는 것 뿐만 아니라
트리의 균형을 자동으로 맞춰주는 로직까지 가지므로 단순하고 효율적이며, 완전히 균형을 맞춘 트리 - 각 노드에는 key와 data가 모두 들어가 저장되게 됨
- 루트 노드는 적어도 2개 이상의 자식을 가져야 하며, 노드의 자료수가 N이면, 자식 수는 N + 1이어야 함
또한 입력 자료는 중복될 수 없음

B+트리란?
- B-트리에서 데이터의 빠른 접근을 위한 인덱스 역할을 하는 비단말 노드가 추가된 트리 자료구조
- 각 노드에는 key만 들어가고, data는 리프 노드에만 존재하게 됨
- 기존의 B-트리(index 부분)와 데이터의 연결리스트(순차 데이터 부분)로 구현된 색인구조로
인덱스 부분의 key 값은 리프 노드에 있는 key 값을 직접 찾아가는데 사용하게 됨

트라이(Trie)란?
- 문자열 검색을 빠르게 실행할 수 있도록 설계한 트리 형태의 자료구조
- Digital Tree, Radix Tree, Prefix Tree라고도 불림
- 단어들을 사전의 형태로 생성한 후 트리의 부모 자식 노드 관계를 이용해 검색을 수행
- 각 노드는 하나의 알파벳인 key와 그 key에 해당하는 자식 노드인 value 값을 가지게 됨
- 문자 종류의 개수인 N에 따라 N진 트리가 결정됨
- 루트 노드는 항상 빈 문자열을 뜻하는 공백 상태를 유지
- 루트 노드를 제외한 노드의 자손들은 해당 노드와 공통 접두어를 가지게 됨

'Tech Interview > Data Structure' 카테고리의 다른 글
| [Data Structure] 그래프 (Graph) (0) | 2023.11.30 |
|---|---|
| [Data Structure] 해시 (Hash) (0) | 2023.11.28 |
| [Data Structure] 힙 (Heap) (0) | 2023.11.25 |
| [Data Structure] 큐 (Queue) (0) | 2023.11.24 |
| [Data Structure] 스택 (Stack) (0) | 2023.11.22 |