핵심 키워드
- #합성곱 #필터 #특성 맵 #패딩 #스트라이드 #풀링
- 합성곱 신경망을 구성하는 기본 개념과 동작 원리를 배우고 간단한 합성곱, 풀링 계산 방법을 익히자
합성곱
- 밀집층
밀집층에는 뉴런마다 입력 개수만큼의 가중치가 있어 모든 입력에 가중치를 곱함
아래의 경우 가중치 w1 ~ w10과 절편 b를 랜덤하게 초기화한 다음 에포크를 반복하면서 경사 하강법 알고리즘을 사용해
손실이 낮아지도록 최적의 가중치와 절편을 찾아냄
밀집층에 뉴런이 3개 있다면 출력은 3개가 됨
즉, 밀집층의 뉴런은 입력 개수만큼 10개의 가중치를 가지고 1개의 출력을 만듦

- 합성곱
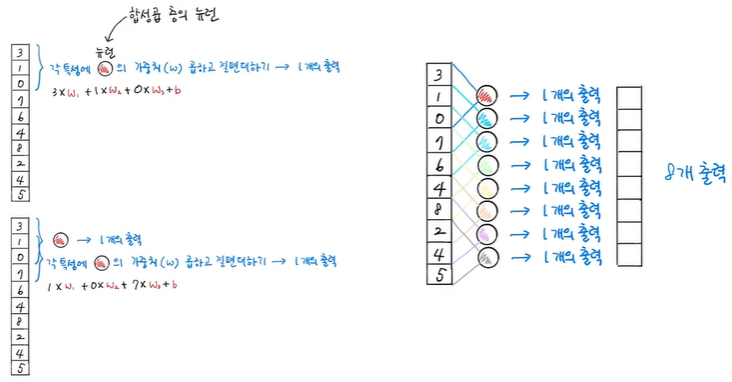
합성곱은 밀집층과 달리, 입력 데이터 전체에 가중치를 적용하는 것이 아니라 일부에 가중치를 곱함
뉴런이 3개의 가중치를 가진다고 가정할 때, 가중치 w1 ~ w3이 입력의 처음 3개 특성과 곱해져 새로운 출력을 만들고
다음으로 이 뉴런이 한 칸 아래로 이동해 두 번째부터 네 번째 특성과 곱해져 새로운 출력을 만듦
이때 첫 번째 합성곱에 사용된 가중치와 절편은 이후 합성곱에도 동일하게 적용하게 됨
이렇게 한 칸씩 아래로 이동하면서 출력을 만드는 것이 합성곱이며 뉴런의 가중치가 3개이기 때문에 출력은 8개
즉, 합성곱 층의 뉴런은 3개의 가중치를 가지고 8개의 출력을 만듦
- 커널 = 필터 = 가중치
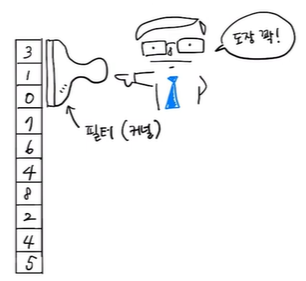
합성곱 신경망(convolutional neural network, CNN)에서는 뉴런을 필터 혹은 커널이라고 부름
뉴런 개수를 이야기할 때는 필터라 부르고, 입력에 곱해지는 가중치를 의미할 때는 커널이라고 부르기도 함
- 2차원 합성곱
합성곱의 장점은 1차원이 아니라 2차원 입력에도 적용할 수 있다는 것
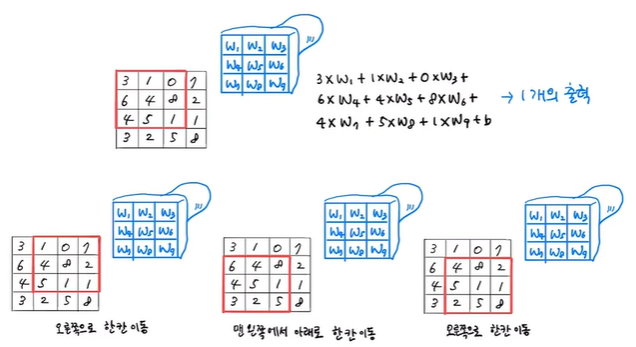
입력이 2차원 배열이면 필터도 2차원이어야 하므로 (4, 4)의 2차원 이미지에 대한 필터의 커널 크기는 (3, 3)
왼쪽 위 모서리에서부터 합성곱을 시작하며, 입력의 9개 원소와 커널의 9개 가중치를 곱하여 1개의 출력을 만듦
그 다음에는 필터가 오른쪽으로 한 칸 이동하여 합성곱을 또 수행하고 더 이상 오른쪽으로 이동할 수 없으면
아래로 한 칸 이동한 다음 다시 왼쪽에서부터 합성곱을 수행하고 다시 오른쪽으로 한 칸 이동
- 특성맵
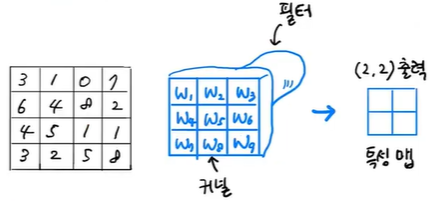
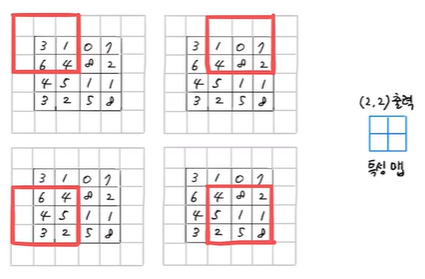
그림에서 필터는 모두 4번 이동할 수 있기 때문에 4개의 출력을 만들며
이때 4개의 출력을 필터가 입력에 놓인 위치에 맞게 2차원으로 배치하게 됨
이렇게 합성곱 계산을 통해 얻은 출력을 특성 맵이라고 부름
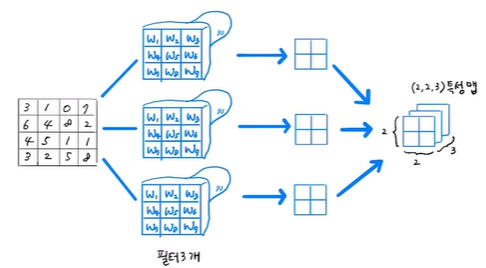
- 여러 개의 필터
밀집층에서 여러 개의 뉴런을 사용하듯이 합성곱 층에서도 여러 개의 필터를 사용함
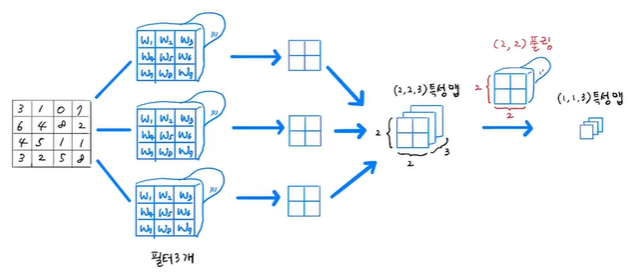
여러 개의 필터를 사용하면 만들어진 특성 맵은 순서대로 차곡차곡 쌓이게 됨
3개의 필터를 사용했을 경우 (2, 2) 크기의 특성 맵이 쌓아져 (2, 2, 3) 크기의 3차원 배열이 됨
(필터 하나가 입력 위를 스캔해 만들어진 결과 차원, 필터의 개수의 차원)
밀집층에 있는 뉴런의 가중치가 모두 다르듯이 합성곱 층에 있는 필터의 가중치(커널)도 모두 다름
케라스 합성곱 층
- 케라스 합성곱 층
케라스의 층은 모두 keras.layers 패키지 아래 클래스로 구현되어 있음
입력 위를 (왼쪽에서 오른쪽으로, 위에서 아래로) 이동하는 합성곱은 Conv2D 클래스로 제공하며
Conv2D 클래스의 첫 번째 매개변수는 필터의 개수이고, 두 번째 kernel_size 매개변수는 필터에 사용할 커널의 크기를 지정함
마지막으로는 밀집층에서처럼 활성화 함수를 지정

- 패딩
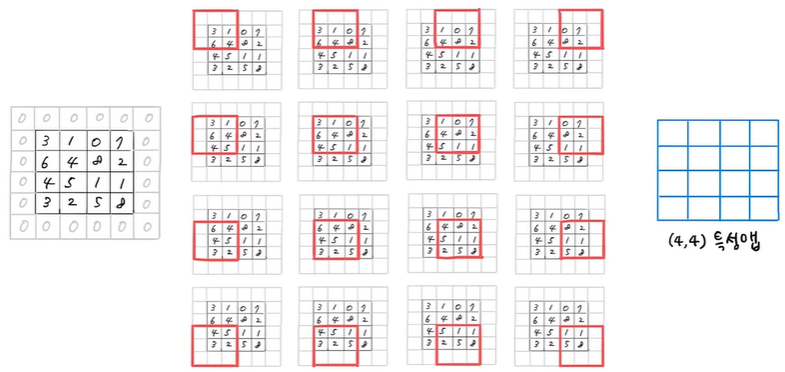
커널 크기는 (3, 3)으로 그대로 두고 출력의 크기를 입력과 동일하게 (4, 4)로 만들려면 패딩을 이용
(4, 4) 입력과 동일한 크기의 출력을 만들려면 마치 더 큰 입력에 합성곱하는 척을 해야하므로
실제 입력 크기는 (4, 4)이지만 (6, 6)처럼 다룬다고 가정하면 (3, 3) 크기의 커널로 합성곱했을 때 출력의 크기가 (4, 4)가 됨
그러므로 왼쪽 위에서 오른쪽 아래까지 한 칸씩 이동하면서 합성곱을 수행하면 입력과 같은 (4, 4) 크기의 출력이 만들어지게 됨
이렇게 입력 배열의 주위를 가상의 원소로 채우는 것을 패딩이라고 함
실제 입력값이 아니기 때문에 패딩은 0으로 채우게 되므로 (4, 4) 크기의 입력에 0을 1개 패딩하면 (6, 6) 크기의 입력이 됨
패딩의 역할을 커널이 도장을 찍을 횟수를 늘려주는 것 밖에 없으며 실제 값은 0으로 채워져 있기 때문에 계산에 영향이 없음
입력과 특성 맵의 크기를 동일하게 만들기 위해 입력 주위에 0으로 패딩하는 것을 세임 패딩
패딩 없이 순수한 입력 배열에서만 합성곱을 하여 특성 맵을 만드는 경우는 밸리드 패딩
- 패딩의 목적
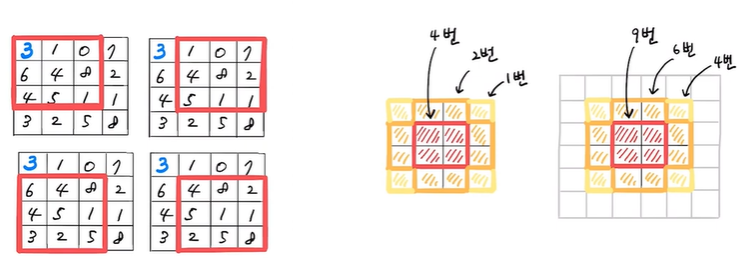
만약 패딩이 없다면 (4, 4) 크기의 입력에 패딩 없이 합성곱을 한다면 왼쪽 위 모서리의 3은 커널 도장에 딱 한 번만 찍히게 됨
이외에도 네 모서리에 있는 다른 3개의 값도 마찬가지로 한 번만 찍히게 되는 반면 다른 원소들은 2번 이상 커널과 계산됨
만약 이 입력을 이미지라고 생각하면 모서리에 있는 중요한 정보가 특성 맵으로 잘 전달되지 않을 가능성이 높게 됨
또한 패딩을 하지 않을 경우 중앙부와 모서리 픽셀이 합성곱에 참여하는 비율이 크게 차이남 (4:1)
그러므로 1픽셀을 하면 차이는 크게 줄며 (9:4), 2픽셀을 하면 중앙부와 모서리 픽셀이 합성곱에 참여하는 비율이 동일해짐 (1:1)
- 케라스의 패딩 설정
케라스 Conv2D 클래스에서는 padding 매개변수로 패딩을 지정할 수 있으며
기본값은 'valid'로 밸리드 패딩을 나타내고, 세임 패딩을 사용하려면 'same'으로 지정
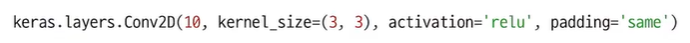
- 스트라이드
합성곱 연산을 좌우, 위아래로 한 칸씩 이동하는 것이 아니라 두 칸씩 건너뛸 수도 있음
이렇게 두 칸씩 이동하면 만들어지는 특성 맵의 크기는 더 작아지게 됨
이런 이동의 크기를 스트라이드라고 함
- 케라스의 스트라이드 설정
케라스의 Conv2D의 기본 스트라이드 값은 1이며 strides 매개변수로 지정 가능

- 풀링
풀링은 합성곱 층에서 만든 특성 맵의 가로세로 크기를 줄이는 역할을 수행함
(2, 2, 3) 크기의 특성 맵에 풀링을 적용하면 마지막 차원인 개수는 유지하고 너비와 높이만 줄어들어 (1, 1, 3) 크기의 특성맵이 됨
즉, 4개의 픽셀이 1개의 픽셀로 압축되는 효과
풀링도 합성곱처럼 입력 위를 지나가면서 도장을 찍으며
풀링에는 가중치가 없으므로 도장을 찍은 영역에서 가장 큰 값을 고르는 최대 풀링이나 평균값을 계산하는 평균 풀링을 적용
- 최대 풀링
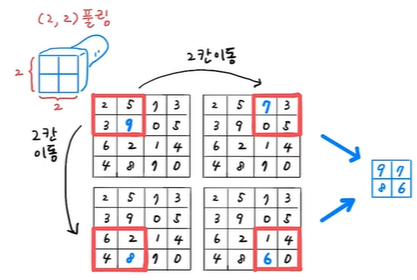
(4, 4) 크기의 특성 맵이 있을 때 (2, 2) 최대 풀링을 적용하면 절반으로 크기가 줄어들게 됨
최대 풀링은 가장 큰 값을 고르므로 첫 번째 (2, 2) 영역에서 9를 고르고 그 다음 7, 8, 6을 차례대로 골라 (2, 2) 크기의 출력을 만듦
이때 필터의 크기가 스트라이드의 크기와 동일하게 움직이므로 2칸씩 겹치지 않게 이동함
또한 풀링은 가로세로 방향으로만 진행하므로 특성 맵의 개수는 변하지 않고 그래도 유지 (채널 차원의 개수는 변경되지 않음)
- 케라스의 풀링 층
MaxPooing2D 클래스로 풀링을 수행하며
첫 번째 매개변수로 풀링의 크기를 지정하며 대부분 풀링 크기는 2로 하여 가로세로 크기를 절반으로 줄이도록 함
또한 합성곱 층과 마찬가지로 strides와 padding 매개변수를 제공하며
strides의 기본값은 자동으로 풀링의 크기이므로 따로 지정할 필요가 없고,
padding의 기본값은 'valid'로 패딩을 하지 않도록 되어 있음

합성곱 신경망의 전체 구조
- 합성곱 신경망
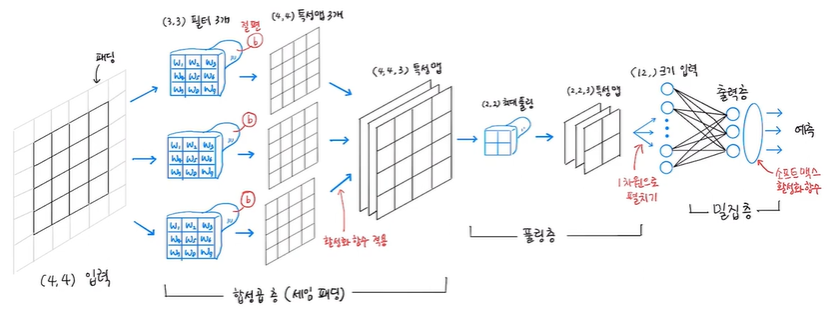
합성곱 층에서 사용할 커널의 크기는 (3, 3) 크기이고 세임 패딩이므로 1픽셀이 입력 데이터 주변에 추가되게 됨 (4, 4) -> (6, 6)
이렇게 패딩이 추가된 입력에서 합성곱이 수행됨
이때 패딩은 텐서플로에서 자동으로 추가하므로 수동으로 입력에 어떤 작업을 추가할 필요가 없음
합성곱의 필터는 3개이므로 각각 (3, 3) 크기의 가중치를 가지고 있으며 필터마다 절편이 하나씩 있음
이러한 필터의 가중치는 각기 서로 다름
따라서 만들어지는 특성 맵의 크기는 입력과 동일한 (4, 4)이며,
3개의 필터가 하나씩 합성곱의 출력을 만들고 이 출력이 쌓여져 (4, 4, 3) 크기의 특성 맵이 만들어짐
밀집층과 마찬가지로 합성곱 층에서 활성화 함수를 적용하므로 렐루 함수를 적용
풀링 층은 합성곱 층에서 만든 특성 맵의 가로세로 크기를 줄이며 보통 (2, 2) 풀링을 사용해 절반으로 줄이며
특성 맵의 개수는 변하지 않아 (4, 4, 3)에서 (2, 2, 3)으로 특성 맵 개수는 유지되게 됨
그후 밀집층인 출력층에 전달하려면 3차원 배열을 1차원으로 펼쳐야하므로
이 배열은 12개의 원소를 가진 1차원 배열이고 출력층의 입력이 되게 됨
출력층에는 3개의 뉴런을 두었으므로 3개의 클래스를 분류하는 다중 분류 문제임
이후 출력층에서 계산된 값은 소프트맥스 활성화 함수를 거쳐 최종 예측 확률이 됨
- 3차원 합성곱 (컬리 이미지를 사용한 합성곱)
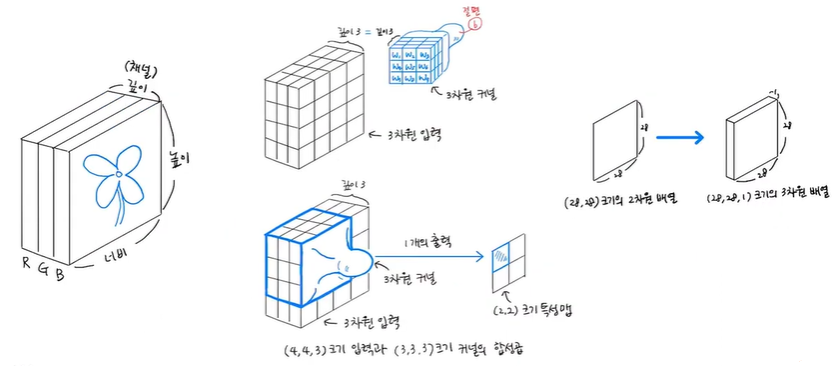
컬러 이미지는 RGB(빨강, 초록, 파랑) 채널로 구성되어 있기 때문에 컴퓨터는 이를 3차원 배열로 표시함
하나의 컬러 이미지는 너비와 높이 차원 외에 깊이 차원 (또는 채널 차원)이 있으므로
입력이 (4, 4)가 아니라 (4, 4, 3)이 되어 마지막 3을 통해 깊이 차원을 표시하게 됨
이렇게 깊이가 있는 입력에서 합성곱을 수행하기 위해서는 도장도 깊이가 필요하므로
필터의 커널 크기는 (3, 3)가 아니라 (3, 3, 3)이 되게 되며 항상 커널 배열의 깊이는 입력의 깊이와 같게 됨
아래의 경우 합성곱의 계산은 (3, 3, 3) 영역에 해당하는 27개의 원소에서 27개의 가중치를 곱하고 절편에 더하는 식이 되며
이때 입력이나 필터의 차원이 몇 개인지 상관없이 항상 출력은 하나의 값이 되어 특성 맵에 있는 한 원소가 채워지게 됨
+)
사실 케라스의 합성곱 층은 항상 3차원 입력을 기대하기 때문에
패선 MNIST 데이터처럼 흑백 이미지일 경우에는 깊이 차원이 1인 3차원 배열로 변환하여 전달하게 됨
예) (28, 28) 크기의 2차원 배열 -> (28, 28, 1) 크기의 3차원 배열로 변환되어 원소 개수는 동일하면서 차원만 맞추게 됨
- 여러 개의 필터가 있는 3차원 합성곱 (합성곱 층, 풀링 층 다음에 다시 또 합성곱 층이 오게 될 때)
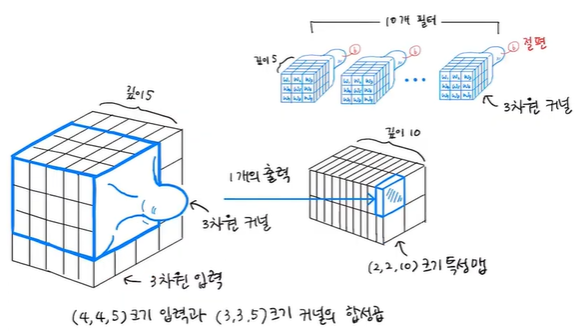
첫 번째 합성곱 층의 필터 개수가 5개일 때, 첫 번째 풀링 층을 통과한 특성 맵의 크기는 (4, 4, 5)라고 함
두 번째 합성곱 층에서 필터의 너비와 높이가 각 3이면 입력의 깊이와 필터의 깊이는 같아야 하므로 필터의 커널 크기는 (3, 3, 5)
그리고 두 번째 합성곱 층의 필터 개수가 10개이기 때문에 합성곱의 결과로 만들어진 1개의 출력인 특성 맵의 크기는 (2, 2, 10)
즉, 입력의 채널 깊이에 모두 적용되어 하나의 출력을 만들어내게 되는 것
이렇게 합성곱 신경망은 너비와 높이는 점점 줄어들고 깊이는 점점 깊어지는 것이 특징이며
이후 마지막에 출력층 전에 특성 맵을 모두 펼쳐서 밀집층의 입력으로 사용함
'ML > 혼자 공부하는 머신러닝 + 딥러닝' 카테고리의 다른 글
| [혼공머신] 08. 이미지를 위한 인공 신경망 - 합성곱 신경망의 시각화 (0) | 2022.07.14 |
|---|---|
| [혼공머신] 08. 이미지를 위한 인공 신경망 - 합성곱 신경망을 사용한 이미지 분류 (0) | 2022.07.13 |
| [혼공머신] 07. 딥러닝을 시작합니다 - 신경망 모델 훈련 (0) | 2022.07.07 |
| [혼공머신] 07. 딥러닝을 시작합니다 - 심층 신경망 (0) | 2022.07.06 |
| [혼공머신] 07. 딥러닝을 시작합니다 - 인공 신경망 (0) | 2022.07.05 |
핵심 키워드
- #합성곱 #필터 #특성 맵 #패딩 #스트라이드 #풀링
- 합성곱 신경망을 구성하는 기본 개념과 동작 원리를 배우고 간단한 합성곱, 풀링 계산 방법을 익히자
합성곱
- 밀집층
밀집층에는 뉴런마다 입력 개수만큼의 가중치가 있어 모든 입력에 가중치를 곱함
아래의 경우 가중치 w1 ~ w10과 절편 b를 랜덤하게 초기화한 다음 에포크를 반복하면서 경사 하강법 알고리즘을 사용해
손실이 낮아지도록 최적의 가중치와 절편을 찾아냄
밀집층에 뉴런이 3개 있다면 출력은 3개가 됨
즉, 밀집층의 뉴런은 입력 개수만큼 10개의 가중치를 가지고 1개의 출력을 만듦

- 합성곱
합성곱은 밀집층과 달리, 입력 데이터 전체에 가중치를 적용하는 것이 아니라 일부에 가중치를 곱함
뉴런이 3개의 가중치를 가진다고 가정할 때, 가중치 w1 ~ w3이 입력의 처음 3개 특성과 곱해져 새로운 출력을 만들고
다음으로 이 뉴런이 한 칸 아래로 이동해 두 번째부터 네 번째 특성과 곱해져 새로운 출력을 만듦
이때 첫 번째 합성곱에 사용된 가중치와 절편은 이후 합성곱에도 동일하게 적용하게 됨
이렇게 한 칸씩 아래로 이동하면서 출력을 만드는 것이 합성곱이며 뉴런의 가중치가 3개이기 때문에 출력은 8개
즉, 합성곱 층의 뉴런은 3개의 가중치를 가지고 8개의 출력을 만듦

- 커널 = 필터 = 가중치
합성곱 신경망(convolutional neural network, CNN)에서는 뉴런을 필터 혹은 커널이라고 부름
뉴런 개수를 이야기할 때는 필터라 부르고, 입력에 곱해지는 가중치를 의미할 때는 커널이라고 부르기도 함

- 2차원 합성곱
합성곱의 장점은 1차원이 아니라 2차원 입력에도 적용할 수 있다는 것
입력이 2차원 배열이면 필터도 2차원이어야 하므로 (4, 4)의 2차원 이미지에 대한 필터의 커널 크기는 (3, 3)
왼쪽 위 모서리에서부터 합성곱을 시작하며, 입력의 9개 원소와 커널의 9개 가중치를 곱하여 1개의 출력을 만듦
그 다음에는 필터가 오른쪽으로 한 칸 이동하여 합성곱을 또 수행하고 더 이상 오른쪽으로 이동할 수 없으면
아래로 한 칸 이동한 다음 다시 왼쪽에서부터 합성곱을 수행하고 다시 오른쪽으로 한 칸 이동

- 특성맵
그림에서 필터는 모두 4번 이동할 수 있기 때문에 4개의 출력을 만들며
이때 4개의 출력을 필터가 입력에 놓인 위치에 맞게 2차원으로 배치하게 됨
이렇게 합성곱 계산을 통해 얻은 출력을 특성 맵이라고 부름

- 여러 개의 필터
밀집층에서 여러 개의 뉴런을 사용하듯이 합성곱 층에서도 여러 개의 필터를 사용함
여러 개의 필터를 사용하면 만들어진 특성 맵은 순서대로 차곡차곡 쌓이게 됨
3개의 필터를 사용했을 경우 (2, 2) 크기의 특성 맵이 쌓아져 (2, 2, 3) 크기의 3차원 배열이 됨
(필터 하나가 입력 위를 스캔해 만들어진 결과 차원, 필터의 개수의 차원)
밀집층에 있는 뉴런의 가중치가 모두 다르듯이 합성곱 층에 있는 필터의 가중치(커널)도 모두 다름

케라스 합성곱 층
- 케라스 합성곱 층
케라스의 층은 모두 keras.layers 패키지 아래 클래스로 구현되어 있음
입력 위를 (왼쪽에서 오른쪽으로, 위에서 아래로) 이동하는 합성곱은 Conv2D 클래스로 제공하며
Conv2D 클래스의 첫 번째 매개변수는 필터의 개수이고, 두 번째 kernel_size 매개변수는 필터에 사용할 커널의 크기를 지정함
마지막으로는 밀집층에서처럼 활성화 함수를 지정

- 패딩
커널 크기는 (3, 3)으로 그대로 두고 출력의 크기를 입력과 동일하게 (4, 4)로 만들려면 패딩을 이용
(4, 4) 입력과 동일한 크기의 출력을 만들려면 마치 더 큰 입력에 합성곱하는 척을 해야하므로
실제 입력 크기는 (4, 4)이지만 (6, 6)처럼 다룬다고 가정하면 (3, 3) 크기의 커널로 합성곱했을 때 출력의 크기가 (4, 4)가 됨
그러므로 왼쪽 위에서 오른쪽 아래까지 한 칸씩 이동하면서 합성곱을 수행하면 입력과 같은 (4, 4) 크기의 출력이 만들어지게 됨
이렇게 입력 배열의 주위를 가상의 원소로 채우는 것을 패딩이라고 함
실제 입력값이 아니기 때문에 패딩은 0으로 채우게 되므로 (4, 4) 크기의 입력에 0을 1개 패딩하면 (6, 6) 크기의 입력이 됨
패딩의 역할을 커널이 도장을 찍을 횟수를 늘려주는 것 밖에 없으며 실제 값은 0으로 채워져 있기 때문에 계산에 영향이 없음
입력과 특성 맵의 크기를 동일하게 만들기 위해 입력 주위에 0으로 패딩하는 것을 세임 패딩
패딩 없이 순수한 입력 배열에서만 합성곱을 하여 특성 맵을 만드는 경우는 밸리드 패딩

- 패딩의 목적
만약 패딩이 없다면 (4, 4) 크기의 입력에 패딩 없이 합성곱을 한다면 왼쪽 위 모서리의 3은 커널 도장에 딱 한 번만 찍히게 됨
이외에도 네 모서리에 있는 다른 3개의 값도 마찬가지로 한 번만 찍히게 되는 반면 다른 원소들은 2번 이상 커널과 계산됨
만약 이 입력을 이미지라고 생각하면 모서리에 있는 중요한 정보가 특성 맵으로 잘 전달되지 않을 가능성이 높게 됨
또한 패딩을 하지 않을 경우 중앙부와 모서리 픽셀이 합성곱에 참여하는 비율이 크게 차이남 (4:1)
그러므로 1픽셀을 하면 차이는 크게 줄며 (9:4), 2픽셀을 하면 중앙부와 모서리 픽셀이 합성곱에 참여하는 비율이 동일해짐 (1:1)

- 케라스의 패딩 설정
케라스 Conv2D 클래스에서는 padding 매개변수로 패딩을 지정할 수 있으며
기본값은 'valid'로 밸리드 패딩을 나타내고, 세임 패딩을 사용하려면 'same'으로 지정
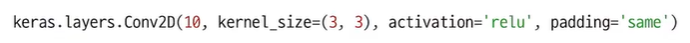
- 스트라이드
합성곱 연산을 좌우, 위아래로 한 칸씩 이동하는 것이 아니라 두 칸씩 건너뛸 수도 있음
이렇게 두 칸씩 이동하면 만들어지는 특성 맵의 크기는 더 작아지게 됨
이런 이동의 크기를 스트라이드라고 함

- 케라스의 스트라이드 설정
케라스의 Conv2D의 기본 스트라이드 값은 1이며 strides 매개변수로 지정 가능

- 풀링
풀링은 합성곱 층에서 만든 특성 맵의 가로세로 크기를 줄이는 역할을 수행함
(2, 2, 3) 크기의 특성 맵에 풀링을 적용하면 마지막 차원인 개수는 유지하고 너비와 높이만 줄어들어 (1, 1, 3) 크기의 특성맵이 됨
즉, 4개의 픽셀이 1개의 픽셀로 압축되는 효과
풀링도 합성곱처럼 입력 위를 지나가면서 도장을 찍으며
풀링에는 가중치가 없으므로 도장을 찍은 영역에서 가장 큰 값을 고르는 최대 풀링이나 평균값을 계산하는 평균 풀링을 적용

- 최대 풀링
(4, 4) 크기의 특성 맵이 있을 때 (2, 2) 최대 풀링을 적용하면 절반으로 크기가 줄어들게 됨
최대 풀링은 가장 큰 값을 고르므로 첫 번째 (2, 2) 영역에서 9를 고르고 그 다음 7, 8, 6을 차례대로 골라 (2, 2) 크기의 출력을 만듦
이때 필터의 크기가 스트라이드의 크기와 동일하게 움직이므로 2칸씩 겹치지 않게 이동함
또한 풀링은 가로세로 방향으로만 진행하므로 특성 맵의 개수는 변하지 않고 그래도 유지 (채널 차원의 개수는 변경되지 않음)

- 케라스의 풀링 층
MaxPooing2D 클래스로 풀링을 수행하며
첫 번째 매개변수로 풀링의 크기를 지정하며 대부분 풀링 크기는 2로 하여 가로세로 크기를 절반으로 줄이도록 함
또한 합성곱 층과 마찬가지로 strides와 padding 매개변수를 제공하며
strides의 기본값은 자동으로 풀링의 크기이므로 따로 지정할 필요가 없고,
padding의 기본값은 'valid'로 패딩을 하지 않도록 되어 있음

합성곱 신경망의 전체 구조
- 합성곱 신경망
합성곱 층에서 사용할 커널의 크기는 (3, 3) 크기이고 세임 패딩이므로 1픽셀이 입력 데이터 주변에 추가되게 됨 (4, 4) -> (6, 6)
이렇게 패딩이 추가된 입력에서 합성곱이 수행됨
이때 패딩은 텐서플로에서 자동으로 추가하므로 수동으로 입력에 어떤 작업을 추가할 필요가 없음
합성곱의 필터는 3개이므로 각각 (3, 3) 크기의 가중치를 가지고 있으며 필터마다 절편이 하나씩 있음
이러한 필터의 가중치는 각기 서로 다름
따라서 만들어지는 특성 맵의 크기는 입력과 동일한 (4, 4)이며,
3개의 필터가 하나씩 합성곱의 출력을 만들고 이 출력이 쌓여져 (4, 4, 3) 크기의 특성 맵이 만들어짐
밀집층과 마찬가지로 합성곱 층에서 활성화 함수를 적용하므로 렐루 함수를 적용
풀링 층은 합성곱 층에서 만든 특성 맵의 가로세로 크기를 줄이며 보통 (2, 2) 풀링을 사용해 절반으로 줄이며
특성 맵의 개수는 변하지 않아 (4, 4, 3)에서 (2, 2, 3)으로 특성 맵 개수는 유지되게 됨
그후 밀집층인 출력층에 전달하려면 3차원 배열을 1차원으로 펼쳐야하므로
이 배열은 12개의 원소를 가진 1차원 배열이고 출력층의 입력이 되게 됨
출력층에는 3개의 뉴런을 두었으므로 3개의 클래스를 분류하는 다중 분류 문제임
이후 출력층에서 계산된 값은 소프트맥스 활성화 함수를 거쳐 최종 예측 확률이 됨

- 3차원 합성곱 (컬리 이미지를 사용한 합성곱)
컬러 이미지는 RGB(빨강, 초록, 파랑) 채널로 구성되어 있기 때문에 컴퓨터는 이를 3차원 배열로 표시함
하나의 컬러 이미지는 너비와 높이 차원 외에 깊이 차원 (또는 채널 차원)이 있으므로
입력이 (4, 4)가 아니라 (4, 4, 3)이 되어 마지막 3을 통해 깊이 차원을 표시하게 됨
이렇게 깊이가 있는 입력에서 합성곱을 수행하기 위해서는 도장도 깊이가 필요하므로
필터의 커널 크기는 (3, 3)가 아니라 (3, 3, 3)이 되게 되며 항상 커널 배열의 깊이는 입력의 깊이와 같게 됨
아래의 경우 합성곱의 계산은 (3, 3, 3) 영역에 해당하는 27개의 원소에서 27개의 가중치를 곱하고 절편에 더하는 식이 되며
이때 입력이나 필터의 차원이 몇 개인지 상관없이 항상 출력은 하나의 값이 되어 특성 맵에 있는 한 원소가 채워지게 됨
+)
사실 케라스의 합성곱 층은 항상 3차원 입력을 기대하기 때문에
패선 MNIST 데이터처럼 흑백 이미지일 경우에는 깊이 차원이 1인 3차원 배열로 변환하여 전달하게 됨
예) (28, 28) 크기의 2차원 배열 -> (28, 28, 1) 크기의 3차원 배열로 변환되어 원소 개수는 동일하면서 차원만 맞추게 됨

- 여러 개의 필터가 있는 3차원 합성곱 (합성곱 층, 풀링 층 다음에 다시 또 합성곱 층이 오게 될 때)
첫 번째 합성곱 층의 필터 개수가 5개일 때, 첫 번째 풀링 층을 통과한 특성 맵의 크기는 (4, 4, 5)라고 함
두 번째 합성곱 층에서 필터의 너비와 높이가 각 3이면 입력의 깊이와 필터의 깊이는 같아야 하므로 필터의 커널 크기는 (3, 3, 5)
그리고 두 번째 합성곱 층의 필터 개수가 10개이기 때문에 합성곱의 결과로 만들어진 1개의 출력인 특성 맵의 크기는 (2, 2, 10)
즉, 입력의 채널 깊이에 모두 적용되어 하나의 출력을 만들어내게 되는 것
이렇게 합성곱 신경망은 너비와 높이는 점점 줄어들고 깊이는 점점 깊어지는 것이 특징이며
이후 마지막에 출력층 전에 특성 맵을 모두 펼쳐서 밀집층의 입력으로 사용함

'ML > 혼자 공부하는 머신러닝 + 딥러닝' 카테고리의 다른 글
| [혼공머신] 08. 이미지를 위한 인공 신경망 - 합성곱 신경망의 시각화 (0) | 2022.07.14 |
|---|---|
| [혼공머신] 08. 이미지를 위한 인공 신경망 - 합성곱 신경망을 사용한 이미지 분류 (0) | 2022.07.13 |
| [혼공머신] 07. 딥러닝을 시작합니다 - 신경망 모델 훈련 (0) | 2022.07.07 |
| [혼공머신] 07. 딥러닝을 시작합니다 - 심층 신경망 (0) | 2022.07.06 |
| [혼공머신] 07. 딥러닝을 시작합니다 - 인공 신경망 (0) | 2022.07.05 |
