핵심 키워드
- #차원 축소 #주성분 분석 #설명된 분산
- 차원 축소에 대해 이해하고 대표적인 차원 축소 알고리즘 중 하나인 PCA(주성분 분석) 모델을 만들어보자
차원과 차원 축소
- 차원 축소
데이터가 가진 속성을 특성이라고 하므로 과일 사진의 경우 10000개의 픽셀이 있기 때문에 10000개의 특성이 있는 것
머신러닝에서는 이런 특성을 차원이라고도 부르므로 10000개의 특성은 결국 10000개의 차원을 뜻함
이 차원을 줄일 수 있다면 저장 공간을 크게 절약할 수 있으며 이를 위한 비지도 학습 중 하나인 차원 축소 알고리즘
차원 축소는 데이터를 가장 잘 나타내는 일부 특성을 선택하여 데이터 크기를 줄이고 지도 학습 모델의 성능을 향상시킴
대표적인 차원 축소 알고리즘으로는 주성분 분석(PCA)가 있음
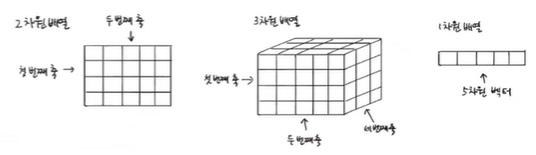
+) 다차원 배열에서 차원은 배열의 축 개수를 뜻하고, 1차원 배열인 벡터에서는 원소의 개수를 말함
주성분 분석 소개
- 주성분
주성분 분석은 데이터에 있는 분산이 큰 방향을 찾는 것을 말함
분산이 큰 방향이란 데이터를 잘 표현하는 어떤 벡터라고 생각할 수 있음
가장 분산이 큰 방향이란 가장 데이터의 분포를 가장 잘 표현하는 방향을 뜻하며 아래 그림에서는 길게 늘어진 대각선 방향
이렇게 찾은 직선이 원점에서 출발한다면 두 원소로 이루어진 벡터인 (2, 1)로 나타낼 수 있음
이러한 벡터를 주성분이라고 부름
원본 데이터는 주성분을 사용해 차원을 줄일 수 있음
예) 2개의 특성이 있는 샘플 데이터 s(4, 2)를 주성분에 직각으로 투영하면 1개의 특성이 있는 1차원 데이터 p(4.5)가 됨
이처럼 주성분은 원본 차원과 같고 주성분으로 바꾼 데이터는 차원이 줄어든다는 점을 알 수 있음
첫 번째 주성분을 찾은 다음 이 벡터에 수직이고 분산이 가장 큰 다음 방향을 찾게 되면 이 벡터가 두 번째 주성분이 됨
일반적으로 주성분은 원본 특성의 개수만큼 찾을 수 있음 (주성분 - 2개, 원본 특성의 개수 - 2개)

PCA 클래스
- PCA
사이킷런은 sklearn.decomposition 모듈 아래 PCA 클래스로 주성분 분석 알고리즘을 제공함
PCA 클래스의 객체를 만들 때 n_components 매개변수에 주성분의 개수를 지정해야 하며
비지도 학습이기 때문에 fit() 메소드에 타깃값을 제공하지 않음
이후 훈련하여 PCA 클래스가 찾은 주성분은 components_ 속성에 저장되어 있음
n_components=50으로 지정했기 때문에 pca.components_ 배열의 첫 번째 차원은 50으로 50개의 주성분을 찾은 것이며
두 번째 차원은 항상 원본 데이터의 특성 개수와 같은 10000
즉, 50개의 주성분은 원본 10000개의 특성이 있는 공간을 가로지는 벡터
그리고 원본 데이터와 차원이 같으므로 주성분을 100 x 100 크기의 이미지처럼 출력할 수 있음
이를 보게 되면 주성분은 원본 데이터에서 가장 분산이 큰 방향을 순서대로 나타낸 것임을 알 수 있음
주성분을 찾았으므로 원본 데이터를 주성분에 투영해 특성의 개수를 10000에서 50개로 줄이기 위해 transform() 메소드 사용
이전의 (300, 10000) 크기의 배열에서 50개의 주성분을 찾은 PCA 모델을 사용하면 (300, 50) 크기의 배열로 변환이 되고
이는 50개의 특성을 가진 데이터라고 할 수 있으며 무려 1/200로 줄어든 것

 01
01
원본 데이터 재구성
- 재구성
위에서 데이터의 차원을 줄였다면 다시 원상 복구할 수 있을까?
특성을 줄이게 되면 어느 정도 손실이 발생할 수밖에 없지만 최대한 분산이 큰 방향으로 데이터를 투영했기 때문에
원본 데이터를 상당 부분 재구성할 수 있음
PCA 클랫는 재구성을 위해 inverse_transform() 메소드를 제공하므로
이를 이용해 50개의 차원으로 축소한 fruits_pca 데이터를 전달해 10000개의 특성을 복원
거의 모든 과일이 잘 복원되었으나 일부 흐리고 번진 부분이 존재함
하지만 불과 50개의 특성을 10000개로 늘린 것을 감안하면 잘 복원된 것
이는 50개의 특성이 분산을 가장 잘 보존하도록 변환된 것이기 때문임


 012
012
설명된 분산
- 설명된 분산
주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지(보존하고 있는지) 기록한 값을 설명된 분산이라고 함
PCA 클래스의 explained_variance_ratio_에는 각 주성분의 설명된 분산 비율이 기록되어 있으며
첫 번째 주성분의 설명된 분산이 가장 크고, 분산 비율을 모두 더하면 50개의 주성분으로 표현하고 있는 총 분산 비율이 됨
이를 확인해보면 92%가 넘는 분산을 유지하고 있는 것을 볼 수 있고
설명된 분산의 비율을 그래프로 그려보면 처음 10개의 주성분이 대부분의 분산을 표현하고 있음을 볼 수 있음

다른 알고리즘과 함께 사용하기
- 분류기와 함께 사용하기
과일 사진 원본 데이터와 PCA로 축소한 데이터를 지도 학습에 적용해보자
지도 학습 모델을 사용하려면 타깃값이 있어야 하므로 사과를 0, 파인애플을 1, 바나나를 2로 지정
이후 원본 데이터인 fruits_2d를 사용해 로직스틱 회귀 모델에서 성능을 가늠해보기 위해 cross_validate()로 교차 검증 수행
교차 검증의 점수는 0.997 정도로 매우 높으며 각 교차 검증 폴드의 훈련 시간이 기록된 fit_time의 경우 1.49초
다음으로는 원본 데이터의 값을 PCA로 축소한 fruits_pca를 사용하면
50개의 특성만 사용했는데도 정확도가 100%이고 훈련 시간은 0.03초
즉, PCA로 훈련 데이터의 차원을 축소하면 저장 공간뿐만 아니라 머신러닝 모델의 훈련 속도도 높일 수 있음
또한 앞서 PCA 클래스를 사용할 때 n_componenets 매개변수에 주성분의 개수를 지정했는데
이 대신 원하는 설명된 분산의 비율을 입력할 수 있어 PCA 클래스는 지정된 비율에 도달할 때까지 자동으로 주성분을 찾게 됨
이를 이용해 분산의 50%에 달하는 주성분을 찾도록 PCA 모델을 만들면 2개의 주성분으로 표현할 수 있음을 알 수 있음
그리고 이 모델로 원본 데이터를 변환하면 데이터의 크기는 (300, 2)가 되며 이를 이용해 교차 검증을 수행하면
2개의 특성을 사용했을 뿐인데도 99%의 정확도를 달성함을 볼 수 있음

 01
01
- 군집과 함께 사용하기
차원 축소된 데이터를 사용해 k-평균 알고리즘으로 클러스터를 찾아보자
fruits_pca로 찾은 클러스터는 각각 110개, 99개, 91개의 샘플을 포함하고 있으므로
앞서 원본 데이터를 사용했을 때와 거의 비슷한 결과를 가짐
KMeans가 찾은 레이블을 사용해 과일 이미지를 출력해 볼 수도 있음
이러한 훈련 데이터의 차원을 줄이는 것은 3개 이하로 차원을 줄이면 화면에 출력하기 쉽기 때문에 시각화라는 장점을 얻음
fruits_pca 데이터는 2개의 특성이 있기 때문에 2차원으로 표현할 수 있으므로
km.labels_를 사용해 클러스터별로 나누어 산점도를 그리면
사과와 파인애플 클러스터의 경계가 가깝게 붙어있어 두 클러스터의 샘플은 몇 개가 혼동을 일으킬 수 있음을 알 수 있음
이처럼 데이터를 시각화하면 예상치 못한 통찰을 얻을 수 있음




 01234
01234
'ML > 혼자 공부하는 머신러닝 + 딥러닝' 카테고리의 다른 글
| [혼공머신] 07. 딥러닝을 시작합니다 - 심층 신경망 (0) | 2022.07.06 |
|---|---|
| [혼공머신] 07. 딥러닝을 시작합니다 - 인공 신경망 (0) | 2022.07.05 |
| [혼공머신] 06. 비지도 학습 - k-평균 (0) | 2022.06.29 |
| [혼공머신] 06. 비지도 학습 - 군집 알고리즘 (0) | 2022.06.28 |
| [혼공머신] 05. 트리 알고리즘 - 트리의 앙상블 (0) | 2022.06.01 |
